様々な因子と死亡のリスク値との関係を推定する際には、しばしばロジスティックモデルや比例ハザードモデルを用いた回帰分析法が採用される。そこで、ここでは、ロジスティック回帰分析法について説明する。26.2 ロジスティック回帰分析法
様々な因子と死亡のリスク値との関係を推定する際には、しばしばロジスティックモデルや比例ハザードモデルを用いた回帰分析法が採用される。そこで、ここでは、ロジスティック回帰分析法について説明する。
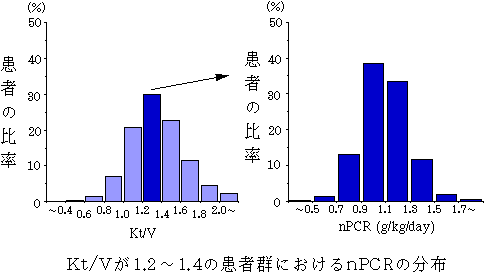
さて、個々の患者の死亡のリスクは、単一の因子ではなく多くの因子により決定されるはずである。これをKt/VとnPCRを例に図を用いて説明する。図では、解析対象患者をKt/V値の0.2ごとにグループ分けし、それぞれのKt/V群に属する患者の比率を棒グラフで示してある。さて、どのKt/V群においてもnPCR値は様々である。例えば、Kt/Vが 1.2 〜1.4 の患者群をとってみると、この群にもnPCR値が0.5 g/kg/day未満の患者からこれが1.7 g/kg/day以上の患者まで様々なnPCR値の患者が含まれている。したがって、様々なKt/V値と様々なnPCR値の組み合わせにより解析対象患者を多くの群に振り分けることができる。
このようにしてグループ分けされたそれぞれの患者群の一定期間後における死亡率は、その患者群に固有のパラメータ値であると解釈できる。今、解析の際の数学的な取り扱いを簡単にするために、グループ分けされたそれぞれの患者群の死亡率を「死亡率（p）と生存率（1-p）の比の自然対数」、すなわちln[p/(1-p)]に変換しておく。通常、ln[p/(1-p)]はロジットと呼ばれる。
さて、ロジット値はKt/Vの寄与による部分とnPCRの寄与による部分とに分けられ、かつロジット値へのKt/VとnPCRの寄与度はそれぞれ、Kt/V値とnPCR値に比例すると仮定すると、次のロジット値の算出式が得られる（ロジスティック関数）。
ln[p/(1-p)] = β0 + β(Kt/V)X(Kt/V) + β(PCR)X(PCR) (1)
ここで、X(Kt/V) とX(PCR) はKt/V値とnPCR値を示し、β(Kt/V) とβ(PCR) はそれぞれ、ロジット値の増減に対するKt/VとnPCRの影響のしやすさ（回帰係数）を示す。ところで、式(1)のβ0 は定数であるが、その意味についてはこの後に述べる。
今、何らかの方法でβ0、β(Kt/V) およびβ(PCR) の値が決定されれば、グループ分けされたどの患者群のロジット値であっても、その患者群のKt/V値とnPCR値を式(1)に代入することにより推定できるはずである。しかし、実際には、そのようにして推定した任意の患者群のロジット値は、その患者群の現実の死亡率から算出したロジット値に完全には一致しないだろう。すなわち、式(1)の右辺を用いてKt/V値とnPCR値から推定したロジット値と式(1)の左辺を用いて実際の死亡率から算出したロジット値とは必ずしも一致せず、その差は患者群ごとに異なると考えられる。
これは、予後に影響を与える因子はKt/VとnPCRだけではないからであると考えられる。そこで、「式(1)の右辺を用いてKt/V値とnPCR値から推定したロジット値」と「式(1)の左辺を用いて実際の死亡率から算出したロジット値」とが完全に一致しないのはやむを得ないと考え、すべての患者群におけるこれらの「推定ロジット値」と「実際ロジット値」との差の絶対値の合計が最小となるようにβ0、β(Kt/V) およびβ(PCR) の値を決定することで満足することとしよう。その際、すべての患者群における「推定ロジット値」と「実際ロジット値」との差の絶対値の合計が小さければ小さいほど、そのロジスティック関数の信頼度は高いことになる。なお、ロジスティック関数には、β(Kt/V) およびβ(PCR) などの回帰係数以外に定数β0 がある。ロジスティック関数では、この定数β0 の値を同時に調整することで、すべての患者群における「推定ロジット値」と「実際ロジット値」との差の絶対値の合計をより小さくすることができる。ロジスティック回帰分析、すなわちロジスティック関数の回帰係数（β(Kt/V)とβ(PCR)）および定数β0 の算出は、市販のロジスティック回帰分析ソフトを用いて行う。
もちろん、このような解析対象患者のグループ分けは、nPCR値とKt/V値だけに基づかなければならないわけではない。Kt/VとnPCRに加えて、血清リン濃度、透析時間、体重増加率、糖尿病の有無、性別、年齢など、多くの因子の値に基づいて患者をグループ分けすることが可能である。その場合には、因子の数だけの回帰係数（β1、β2、・・・βnの値）が存在することになる。しかし、たとえ十数個の因子を含むロジスティック関数であっても、市販のロジスティック回帰分析ソフトを用いれば解析することができる。
死亡の相対危険度に続く。
