1. nPCR(蛋白質異化率)
蛋白質摂取量を反映するnPCRは、尿素の産生速度から算出され、尿素の産生速度は 単位体液量、例えば 1 mL の血液に含まれる尿素の量である。尿素窒素濃度(BUN)から求める。そして、 理論的に血清尿素窒素濃度から求めた尿素の産生速度は単位体液量あたりの尿素産生速度となる。したがって、ある患者における総尿素産生速度を求めようとする場合には、 血清尿素窒素濃度から求めた尿素産生速度を体液量と掛け合わせなければならない。
ということは、正確な nPCR を算出するためには、正確な体液量が必要であることになる。しかし、現在しばしば用いられる透析後体重の 58% としている体液量は、実際にはほとんどの患者で真の体液量に対して過大評価されている。
2. 尿素分布容積の精度
尿素は、安定状態では体液のすべての区画に均一の濃度で分布する。これは体液量は実質的に尿素分布容積に等しいことを意味している。
現時点で臨床的に可能な尿素分布容積(体液量)を求める方法のうち、もっとも正確なものは、透析によって除去された実測の尿素の総量を透析前後の血清尿素窒素濃度の差で割ることである。 山本らは、この方法で求めた体液量を対照として、種々の方法で求めた体液量の正確さを比較し、図1に示すように、尿素動態モデルを解析することによってダイアライザの尿素クリアランス、透析時間、透析前後の 血清尿素窒素濃度から算出した尿素分布容積が最も正確であり、次に正確なのは Watson の式を用いて性別、年齢、身長、体重から算出した尿素分布容積であったとの結論を得ている。さらに、彼らは、もっとも精度が劣るのは透析後体重の 58% として求めた尿素分布容積であったとも報告している。
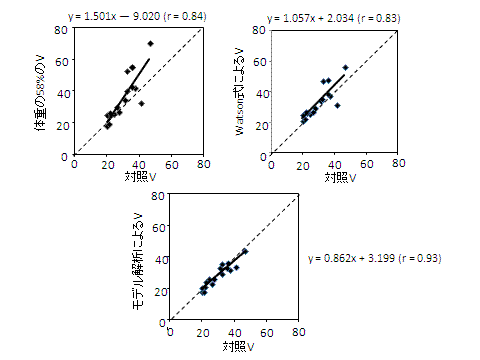
図1 尿素分布容積(x)とそれぞれ異なる方法で求めた尿素分布容積(y)との関係.
点線はy=x を示す。
3. nPCRの精度
nPCR を求める山本らの
簡易
式では、体液量を透析後体重の
58% として nPCR
を算出している。ところが、すでに述べたように、もっとも正確な体液量はダイアライザの尿素クリアランス、透析時間、透析前後の血清尿素窒素濃度から算出した尿素分布容積である。したがって、nPCR
を求める山本らの簡易式で、透析後体重の 58%
として求めた体液量の代わりにダイアライザの尿素クリアランス、透析時間、透析前後の血清尿素窒素濃度から算出した尿素分布容積を用いれば、より正確な nPCR
が算出されることになる。
さて、実用性は無視することにして、現時点でもっとも正確な nPCR を求める方法は、透析によって除去された実測尿素窒素量を透析前後の血清尿素窒素濃度の差で割ることにより求めた尿素分布容積と、透析終了時から次回の透析開始時までの間の血 清尿素窒素濃度の上昇度から求めた尿素産生速度の2つの要素を使用して求めた nPCR であろう。山本らは、この方法で求めた nPCR とその他、種々の方法で求めた nPCR とを比較することにより、より正確な nPCR を求める方法を明らかにしている [1]。
彼らは、図2に示すように、もっとも正確なのは、尿素動態モデルを解析することによりダイアライザの尿素クリアランス、透析時間、透析前後の血清尿素窒素濃度から求めた尿素分布容積に基づく nPCR であり、次に正確なのは Watson の式を用いて性別、年齢、身長、体重から算出した尿素分布容積に基づく nPCR であるとしている。そして、もっとも正確さが劣るのは、尿素分布容積を透析後体重の 58% として求めた nPCR であったと報告している。
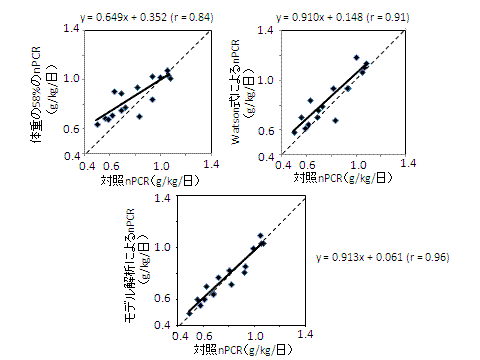
図2 実測尿素分布容積に基づくnPCR(x)とそれぞれ異なる方法で求めた
尿素分布容積に基づくnPCR(y) との関係. 点線は y=x を示す。
4. 尿素動態モデルを解析することにより得られた尿素分布容積に基づく nPCR の算出式
図3には、nPCR を求める山本らの簡易式と尿素動態モデルを解析して尿素分布容積を求める式とを組み合わせることにより作成した nPCR (g/kg/日) を算出する新しい式を示す(仮に単に山本の式としておく)。山本の式では、R は透析開始時における血清尿素窒素濃度に対する透析終了時における血清尿素窒素濃度の比、TD は透析時間(分)、(G/V)1 は体重変化を無視した時の尿素産生速度(g/V/分)、(G/V)2 は体重変化で補正した尿素産生速度 (g/V/分)、V は尿素分布容積 (L)、BW は透析終了時の体重 (kg)、?BWは透析中の体重減少量 (kg)、CS1 は週の最初の透析開始時の血清尿素窒素濃度 (g/L)、QB は血流量 (ml/分)、QD は透析液流量(ml/分)、KoA は尿素に関する総括物質移動面積係数 (ml/分) を示す。式 (5) では、ml/ 分単位の QB、QD および KoA から算出した V をリットル単位で表示するために、式全体を 1000 で割っている。また、KoAは、メーカーのダイアライザのカタログに記載されている尿素のクリアランスから表1に従って求める。
なお、上記の式を導く具体的な過程については文献 [1] を参照されたい。
以下に、山本の式を基に作成した新しいnPCR を求めるためのコンピュータ・プログラムを示す。
10 REM ***** nPCRプログラム
*****
20 INPUT”カタログの尿素クリアランス(mL/分)=”;KS
30 IF 150=<KS AND KS=<179 THEN KOA =0.147*KS^2-39.574*KS+2974.9
40 IF 179<KS AND KS=<190 THEN KOA=0.789*KS^2-270.12*KS+23678
50 IF 190<KS AND KS=<197 THEN KOA=5.369*KS^2-2024.6*KS+191709
60 IF 197<KS AND KS=<200 THEN KOA=268.5*KS^2-106365*KS+10535363
70 INPUT”透析時間(hr)=”;T
80 TD=T*60
90 INPUT”血流量(mL/分)=”;QB
100 INPUT”透析液流量(mL/分)=”;QD
110 INPUT”透析前体重(kg)=”;BW1
120 INPUT”透析後体重(kg)=”;BW2
130 INPUT”透析前BUN(mg/dL)=”;CU1
140 CU1=CU1/100
150 INPUT”透析後BUN(mg/dL)=”;CU2
表1
160 CU2=CU2/100
170 IF QD=QB THEN QD=QD+0.1
180 AA=1-EXP(KOA*(1/QB-1/QD))
190 BB=1/QD-1/QB*EXP(KOA*(1/QB-1/QD))
200 K=AA/BB
210 K=K*0.66
220 V=-K*TD/LOG(CU2/CU1) :’(ここでのLOGは自然対数)
230 V=V/1000
240 A=1.0171* (CU2/CU1- 0.000133*TD)^ 0.99
250 W1= (1-A)+ CU2/CU1*(1-A^2)
260 W2= 10080-3*TD+(A^2+A-2)*(2880-TD+TD/LOG(A)) :’ (ここでのLOGは自然対数)
270 GV=W1/W2*CU1
280 GV2=GV+(BW1-BW2)/V*CU1/(60*72-TD)
290 GV2=GV2*1000
300 R=V/BW2
310 PCR=9.35*R*GV2+0.29*R
320 PRINT”nPCR(g/kg/日)=”;PCR
5. BMI と尿素分布容積/体重比が 58% と一定であるとして求めた nPCR との関係
図4に示すように、BMI(x) と透析後体重 1 kg あたりの尿素分布容積 (y) との間には、以下に示す有意の負の相関が認められた (r=0.67、P<0.01)。
y = -0.871 x + 71.62
この結果は、BMI が大きい患者ほど、つまり太っている患者ほど、透析後体重 1 kg あたりの尿素分布容積が小さいことを示している。したがって、尿素分布容積 /体重比は 58% と一定であるとすると、尿素分布容積は BMI が高い患者で過大評価され、BMI が低い患者で過小評価されることになる。
上記の BMI(x) と透析後体重 1 kg あたりの尿素分布容積の比率 (y) との関係を示す上記の式によると、尿素分布容積 / 体重比が 58% のときの BMI は 15.6kg/? である。そして、平均的なBMIは 22kg/? なので、これは、尿素分布容積 / 体重比を 58% とすると、ほとんどの患者では nPCR が過大評価されることを意味している。
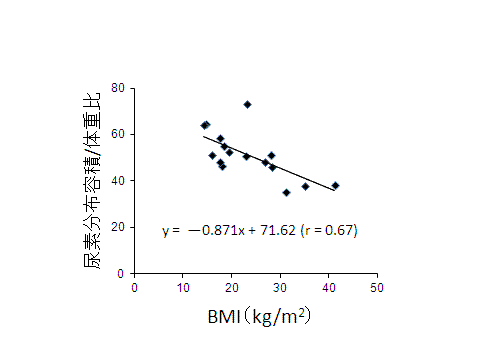
図4 BMI(x) と尿素分布容積/体重比(y) との関係

